https://www.youtube.com/watch?v=PFs0JR-moRo&list=PLvD34F0ZVsoqApURhwM1j4IJGDDoKxGp3
Desarrollar una superficie es extenderla sobre un plano. Cada cara de la figura gira hasta quedar perfectamente coplanaria con la adyacente.
En el dibujo observamos como la caja empieza a abrir sus caras hasta que para que se produzca el desarrollo o extensión sobre el plano deben ser todas coincidentes en el mismo.
Animación de apertura de caras para posterior desarrollo
 Desarrollo de la figura anterior (extensión de sus caras sobre un plano).
Desarrollo de la figura anterior (extensión de sus caras sobre un plano).Ejemplos de poliedros irregulares en planta y alzado con su desarrollo:
Prisma oblicuo:Desarrollo de pirámide tetraédrica con doble truncamiento:
Desarrollo de pirámide de base pentagonal regular con truncamiento de extremo superior:
---------------------------------------------------------------
Desarrollo de una pirámide
 Para hacer el desarrollo de una pirámide sólo hay que abatir sus caras. Para abatir la cara azul de la pirámide consideramos el plano vertical que contiene a la proyección de este punto V sobre la base. Donde éste plano vertical corta a la cara de la figura VC se hace centro en C con la distancia VC hasta el vértice V de la figura. Este giro en el espacio del vértice de la figura intercepta a la línea de intersección C-(V) del plano vertical con el plano de la base en el punto abatido (V).
Para hacer el desarrollo de una pirámide sólo hay que abatir sus caras. Para abatir la cara azul de la pirámide consideramos el plano vertical que contiene a la proyección de este punto V sobre la base. Donde éste plano vertical corta a la cara de la figura VC se hace centro en C con la distancia VC hasta el vértice V de la figura. Este giro en el espacio del vértice de la figura intercepta a la línea de intersección C-(V) del plano vertical con el plano de la base en el punto abatido (V).
Este giro que hemos hecho en el espacio lo podemos hacer en planta por lo que el plano vertical es el que se abate poniendo la altura h en planta y la operación de girar el vértice V de la figura se hace sobre el plano de la planta.
 En la figura observamos en planta como se hace el abatimiento de la cara azul, a partir de la proyección del vértice en planta colocamos la altura en una paralela a la arista de la base MN. haciendo centro en el punto C y tomando como radio la distancia desde este punto hasta el extremo de la altura (V') hacemos un marco hasta que corte a la perpendicular a MN por V' .
En la figura observamos en planta como se hace el abatimiento de la cara azul, a partir de la proyección del vértice en planta colocamos la altura en una paralela a la arista de la base MN. haciendo centro en el punto C y tomando como radio la distancia desde este punto hasta el extremo de la altura (V') hacemos un marco hasta que corte a la perpendicular a MN por V' .
Una vez que obtenemos el vértice abatido (V) lo unimos con los dos extremos MN del la arista de la figura. Haciendo centro en cada uno de estos extremos y tomando como radio para los arcos de las aristas del nuevo triángulo abatido azul interceptamos en la intersección de estos dos arcos bc con las perpendiculares desde el vértice V a los lados de la base del triángulo los vértices W Q de las otras dos caras abatidas.
 En la figura observamos como un cubo empieza a desplegar sus caras para generar próximamente un desarrollo o extensión sobre el plano.
En la figura observamos como un cubo empieza a desplegar sus caras para generar próximamente un desarrollo o extensión sobre el plano. A la hora de hacer el desarrollo del cubo hay que tener en cuenta los puntos que son coincidentes en el giro de las caras. por ejemplo, en la figura, mediante el giro de dos caras unidas por el vértice vemos que los puntos BB son coincidentes con un simple giro de 90° de las cargas unos respecto a la que tienen al lado. En el caso del punto A ya es más complicado, hay que girar las cuatro caras 90°, teniendo en cuenta que la cara más alejada gira primero con la cara adyacente otros 90°, con lo que al final esta cara gira 180°.
A la hora de hacer el desarrollo del cubo hay que tener en cuenta los puntos que son coincidentes en el giro de las caras. por ejemplo, en la figura, mediante el giro de dos caras unidas por el vértice vemos que los puntos BB son coincidentes con un simple giro de 90° de las cargas unos respecto a la que tienen al lado. En el caso del punto A ya es más complicado, hay que girar las cuatro caras 90°, teniendo en cuenta que la cara más alejada gira primero con la cara adyacente otros 90°, con lo que al final esta cara gira 180°. En la figura observamos un cilindro ensistema diédrico y su desarrollo en color amarillo. Observamos en el desarrollo que la altura del mismo permanece invariable así como las dos circunferencias del mismo. La superficie cilíndrica se transforma al desarrollarse en un rectángulo cuyo lado de la base k corresponde a la longitud de la circunferencia: el radio por dos y por pi, esto es el diámetro por pi, lo que se llama la rectificación de la circunferencia, gráficamente la podemos obtener tomando el diámetro y dibujándolo 3,14 veces, uno a continuación del otro. Para hacerlo gráficamente sobre una línea marcamos con el compás el primer diámetro a continuación el siguiente y luego el siguiente, a continuación tomamos un cuarto diámetro y por el teorema de Thales lo dividimos en 10 partes de las que cogemos 1,4.
En la figura observamos un cilindro ensistema diédrico y su desarrollo en color amarillo. Observamos en el desarrollo que la altura del mismo permanece invariable así como las dos circunferencias del mismo. La superficie cilíndrica se transforma al desarrollarse en un rectángulo cuyo lado de la base k corresponde a la longitud de la circunferencia: el radio por dos y por pi, esto es el diámetro por pi, lo que se llama la rectificación de la circunferencia, gráficamente la podemos obtener tomando el diámetro y dibujándolo 3,14 veces, uno a continuación del otro. Para hacerlo gráficamente sobre una línea marcamos con el compás el primer diámetro a continuación el siguiente y luego el siguiente, a continuación tomamos un cuarto diámetro y por el teorema de Thales lo dividimos en 10 partes de las que cogemos 1,4.Para rectificar una circunferencia que es lo mismo que extenderla o convertirla en una línea recta, se coge la circunferencia azul y por el centro A se traza una recta i que forme 30 grados con la vertical BQ. Esa recta corta a la tangente j en el punto O.
A partir de ese punto tomamos tres veces el radio hasta que obtenemos el punto P
Unimos el punto P con el punto Q y esa es la longitud de la semicircunferencia, si duplicamos la medida tendremos la longitud de toda la circunferencia.
Rectificar la circunferencia nos sirve para desarrollar figuras que contienen circunferencias como puede ser un cilindro.
 En la figura observamos el desarrollo de un cono. El cono en el sistema diédrico a la izquierda aparece con dos medidas, 10 unidades para el radio de la base y en el alzado observamos que tiene 60 unidades para la generatriz, definida mediante un arco de circunferencia en color rojo. Para hacer el desarrollo de la superficie de revolución tenemos que hacer un sector circular cuyo radio es igual que la generatriz del cono y cuyo ángulo se puede obtener mediante una regla de tres, teniendo en cuenta que la longitud del arco del sector es igual a la longitud de la circunferencia de la base.
En la figura observamos el desarrollo de un cono. El cono en el sistema diédrico a la izquierda aparece con dos medidas, 10 unidades para el radio de la base y en el alzado observamos que tiene 60 unidades para la generatriz, definida mediante un arco de circunferencia en color rojo. Para hacer el desarrollo de la superficie de revolución tenemos que hacer un sector circular cuyo radio es igual que la generatriz del cono y cuyo ángulo se puede obtener mediante una regla de tres, teniendo en cuenta que la longitud del arco del sector es igual a la longitud de la circunferencia de la base.
De esta forma 2 por pi por la generatriz será a 360º como 2 por pi por el radio de la circunferencia de la planta será a equis ángulos. X por tanto será igual a 360º por el radio de la circunferencia de la base partido por la generatriz del cono dada en el alzado.
Podemos comprobar que siendo el radio de la circunferencia en planta un sexto de la generatriz del cono, el ángulo de la figura desarrollada correspondiente al sector circular será un sexto, pues hay una relación entre el radio de la circunferencia de la base a la generatriz como del sector a la circunferencia.
Casos particulares de desarrollos del cono:

Casos particulares de desarrollos del cono:

Izquierda (A'-cono, A-desarrollo): si el radio de la base del cono es 1 y su generatriz 2 tenemos que 1 es a 2 como el arco desarrollado x es a la circunferencia de 360º de la base.
1/2 = x/ 360º , de donde x= 1. 360º/ 2, por tanto x=180º.
El sector circular tiene por lado el valor de la generatriz del cono (3) y por arco 180º.
Centro (B'-cono, B-desarrollo): si el radio de la base del cono es 1 y su generatriz 3 tenemos que 1 es a 3 como el arco desarrollado x es a la circunferencia de 360º de la base.
1/3 = x/ 360º , de donde x= 1. 360º/ 3, por tanto x=120º.
El sector circular tiene por lado el valor de la generatriz del cono (3) y por arco 120º.
Derecha (C'-cono, C-desarrollo): si el radio de la base del cono es 1 y su generatriz 4 tenemos que 1 es a 4 como el arco desarrollado x es a la circunferencia de 360º de la base.

Derecha (C'-cono, C-desarrollo): si el radio de la base del cono es 1 y su generatriz 4 tenemos que 1 es a 4 como el arco desarrollado x es a la circunferencia de 360º de la base.
1/4 = x/ 360º , de donde x= 1. 360º/ 4, por tanto x=90º.
El sector circular tiene por lado el valor de la generatriz del cono (3) y por arco 90º.
Desarrollo del cono truncado:

Desarrollo de un cono para proyectar el hemisferio norte sobre el mismo, en una proyección cartográfica cónica
Cogemos el radio de la base del cono qué es 1,41 por ser la hipotenusa tangente a la esfera en el paralelo 45 grados. Tenemos por tanto que la hipotenusa vale 2 unidades.
1,41 el radio de la base del cono es a 2 unidades - la hipotenusa - como el ángulo del sector circular que va a ser desarrollo del cono es a 360 grados. De esta manera podemos observar que el ángulo del sector circular- en amarillo- corresponde a 253.8º
 El desarrollo de una letra T, en la que debemos cuidar que el giro de las caras para que no interfieran entre sí.
El desarrollo de una letra T, en la que debemos cuidar que el giro de las caras para que no interfieran entre sí. Hay distintas soluciones para la misma figura, tenemos que tener en cuenta que para que se lleve a efecto el desarrollo la figura deberíamos poder construirla por ejemplo en papel, por lo que sus caras no se pueden superponer, esto quiere decir que la cara adyacente a otra cara no se puede solapar como otra cara que esté adyacente a la última.
Hay distintas soluciones para la misma figura, tenemos que tener en cuenta que para que se lleve a efecto el desarrollo la figura deberíamos poder construirla por ejemplo en papel, por lo que sus caras no se pueden superponer, esto quiere decir que la cara adyacente a otra cara no se puede solapar como otra cara que esté adyacente a la última. Figura en forma de L en la que es incipiente el giro de las caras hasta completar más adelante el desarrollo de la figura.
Figura en forma de L en la que es incipiente el giro de las caras hasta completar más adelante el desarrollo de la figura. Desarrollo de una superficie prismática con un grosor dado de chapa y sección de la misma para indicar un detalle del grosor.
Desarrollo de una superficie prismática con un grosor dado de chapa y sección de la misma para indicar un detalle del grosor. En la figura observamos otra superficie prismática con su correspondiente desarrollo. El detalle cilíndrico hueco enlazado con una cara de la figura mediante una superficie de doble curvatura llamada escocia no es desarrollable, por lo que no aparece en el desarrollo de la figura.
En la figura observamos otra superficie prismática con su correspondiente desarrollo. El detalle cilíndrico hueco enlazado con una cara de la figura mediante una superficie de doble curvatura llamada escocia no es desarrollable, por lo que no aparece en el desarrollo de la figura. Otro detalle de una figura de chapa en la que observamos elementos como las líneas por las que se dobla la superficie que aparecen mediante segmentos mayores y menores alternos.
Otro detalle de una figura de chapa en la que observamos elementos como las líneas por las que se dobla la superficie que aparecen mediante segmentos mayores y menores alternos. Otra figura de chapa que representa un prisma hueco de base pentagonal regular y un posible desarrollo de la misma.
Otra figura de chapa que representa un prisma hueco de base pentagonal regular y un posible desarrollo de la misma. Otro prisma pero sin tener en consideración el grosor de las caras por lo que es una superficie "enteramente" plana como por ejemplo, la que podría corresponder a una figura de papel.
Otro prisma pero sin tener en consideración el grosor de las caras por lo que es una superficie "enteramente" plana como por ejemplo, la que podría corresponder a una figura de papel. Otro detalle de desarrollo de prisma de base triangular equilátera con un el doblaje en las aristas superiores y con un detalle a mayor escala, este detalle refleja la escala del objeto original, no la del dibujo que tiene al lado.
Otro detalle de desarrollo de prisma de base triangular equilátera con un el doblaje en las aristas superiores y con un detalle a mayor escala, este detalle refleja la escala del objeto original, no la del dibujo que tiene al lado. Figura desarrollada sobre un plano con una posible solución en la colocación de las caras para que no interfieran entre sí. El rayado discontinuo entre caras muestra la línea por donde se debe recortar recortar.
Figura desarrollada sobre un plano con una posible solución en la colocación de las caras para que no interfieran entre sí. El rayado discontinuo entre caras muestra la línea por donde se debe recortar recortar. En el dibujo se ve el giro de las caras de una T que puede dar lugar a continuación al desarrollo de la figura.
En el dibujo se ve el giro de las caras de una T que puede dar lugar a continuación al desarrollo de la figura. En la figura observamos el desarrollo de la figura anterior a la izquierda, en el centro podemos ver cómo se empiezan a plegar las caras hasta construir en una proyección ortogonal a la derecha la figura.
En la figura observamos el desarrollo de la figura anterior a la izquierda, en el centro podemos ver cómo se empiezan a plegar las caras hasta construir en una proyección ortogonal a la derecha la figura. Para la comprensión de las figuras cuando se hace el giro de las caras de la superficie desarrollada conviene dar distintos colores según sea la superficie interna o externa de la figura. En la figura podemos observar el exterior en color rojo y la parte interna de la superficie desarrollada en color verde.
Para la comprensión de las figuras cuando se hace el giro de las caras de la superficie desarrollada conviene dar distintos colores según sea la superficie interna o externa de la figura. En la figura podemos observar el exterior en color rojo y la parte interna de la superficie desarrollada en color verde.
Sistema americano a la derecha y europeo a la izquierda
Desarrollo del prisma
--------------------------------------------------------------------------------------------------------
Desarrollo de poliedros regulares:
Poliedros regulares son aquellos que tienen por caras polígonos regulares, los polígonos regulares son los que tienen los lados y ángulos iguales.
Todos se pueden inscribir y circunscribir en esferas, también se pueden inscribir unos dentro de otros y la forma más fácil de dibujarlos es dibujando primero el más sencillo, que es el cubo, e inscribirlo dentro de esta figura.
Poliedros duales son aquellos que tienen vértices y caras intercambiados, por ejemplo, el octaedro regular tiene seis vértices y ocho caras mientras que el cubo tiene ocho vértices y seis caras.
El dodecaedro regular tiene 12 caras que son pentágonos regulares, tiene asimismo 20 vértices.
El icosaedro regular, dual del anterior, tiene 20 caras que son triángulos equiláteros y 12 vértices.
El octaedro regular tiene ocho caras que son triángulos equiláteros y seis vértices
Otras vistas del cubo. El cubo o hexaedro regular, es una figura que tiene seis caras cuadradas, con 8 vértices y seis caras.
Tetraedro regular
El tetraedro regular, que es dual de sí mismo, tiene cuatro vértices y cuatro caras. Si cogemos los puntos medios de cada cara y los unimos mediante aristas que comprendan las distancias más cortas, obtenemos otro tetraedro regular invertido.
Dipirámides: https://dipiramides.blogspot.com/
Deltoedros: https://deltoedros.blogspot.com/
--------------------------------------------------------------------------------------------------------
En el teorema de Euler de los poliedros convexos tenemos que:
V + C = A + 2
Vértices más caras es igual a aristas +2, esto nos sirve para obtener alguno de esos elementos si tenemos los otros dos.
-------------------------------------------------------------------------------------------------
Desarrollo de poliedros arquimedianos:
Truncamiento de tipo 1: a 1/2 de la arista
Truncamiento de tipo 2: el que deja la arista centrada del nuevo poliedro sobre la cara que se corta.
 Tetraedro truncado. Poliedro arquimediano obtenido del truncamiento de tipo 2 de un tetraedro regular.
Tetraedro truncado. Poliedro arquimediano obtenido del truncamiento de tipo 2 de un tetraedro regular.
Esta figura tiene 12 vértices y 18 paristas, así como ocho caras que corresponden a cuatro triángulos + 4 hexágonos.
 Cubo truncado. Poliedro arquimediano obtenido del truncamiento de tipo 2 de un cubo. Esta figura tiene 24 vértices y 38 aristas, tiene además 14 caras comprendidas entre ocho triángulos + 6 octógonos
Cubo truncado. Poliedro arquimediano obtenido del truncamiento de tipo 2 de un cubo. Esta figura tiene 24 vértices y 38 aristas, tiene además 14 caras comprendidas entre ocho triángulos + 6 octógonos
Otra vista de la figura anterior
Cuboctaedro. Poliedro arquimediano obtenido del truncamiento de tipo 1 de un cubo. Esta figura tiene 12 vértices y 24 aristas, tiene además 14 caras que son ocho triángulos +6 cuadrados.
 Cuboctaedro rombitruncado. La figura anterior según otra disposición. Esta figura tiene 48 vértices y 72 artistas, tiene además 26 caras, de las cuales ocho son hexágonos, 12 son cuadrados y seis son octógonos
Cuboctaedro rombitruncado. La figura anterior según otra disposición. Esta figura tiene 48 vértices y 72 artistas, tiene además 26 caras, de las cuales ocho son hexágonos, 12 son cuadrados y seis son octógonosCuboctaedro rombitruncado (p. arquimediano) en dodecaedro disdiakis (p. de Catalan)
Rombicuboctaedro. Pieza anterior con perspectiva. Esta figura tiene 24 vértices y 48 aristas, tiene además 26 caras de las que ocho son triángulos equiláteros y 18 son cuadrados
Octaedro truncado. Poliedro arquimediano obtenido del truncamiento de tipo 2 de un octaedro regular. Esta figura tiene 24 vértices y 36 artistas, tiene además 14 caras de las que ocho son hexágonos y seis son cuadrados.
El poliedro anterior con perfil y perspectiva axonométrica
Aquí se ve cómo se puede dibujar el octaedro truncado partiendo de un octaedro regular
Octaedro truncado con tres proyecciones en planta, alzar y perfil idénticas.
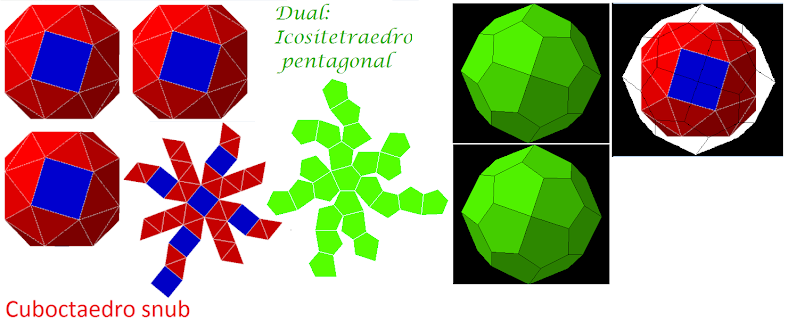
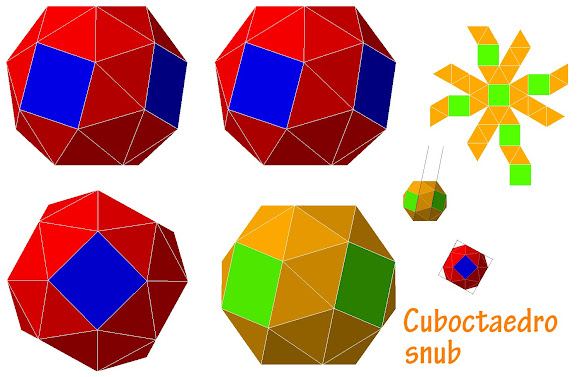
Esta figura denominada cubo romo o snub o chato, también se denomina cuboctaedro snub.
Tiene 24 vértices y 60 artistas, el número de caras es 38, está constituido por 32 triángulos y seis cuadrados.
Su dual, el icositetraedro pentagonal de 24 caras, 60 aristas y 38 vértices, con los vértices del cuboctaedro snub centrado en sus caras
------------------------------------------------------------
Icosidodecaedro snub. Esta figura, denominada también dodecaedro romo, está formada por 60 vértices y 150 aristas, el número de caras es 92, constituida por 80 triángulos y 12 pentágonos
Otras vistas de la figura anterior.
El hexecontaedro pentagonal dual del icosidodecaedro snub e inscrito en él
Otra posición del poliedro icosidodecaedro snub o romo inscrito en el hexecontaedro pentagonal (60 pentágonos irregulares) y desarrollo del hexecontaedro pentagonal.
---------------------------------------------------------------
El icosidodecaedro tiene 30 vértices y 60 aristas, tiene además 32 caras de las que 20 son triángulos y 12 son pentágonos.
El rombicosidodecaedro tiene 60 vértices y 120 artistas, tiene además 62 caras que son 20 triángulos + 30 cuadrados más 12 pentágonos.
Rombicosidodecaedro inscrito en su dual de Catalan: hexecontaedro deltoidal
Gran Rombicosidodecaedro inscrito en dodecaedro.
--------------------------------------------------------------------------------------------------------
Desarrollo de poliedros de Catalan (duales de arquimedianos):
Son poliedros duales y por tanto tienen el mismo número de aristas que los arquimedianos mientras que el número de vértices y caras los tienen intercambiados. Por ejemplo si el tetraedro truncado tiene 12 vértices y ocho caras, su dual, el tetraedro tetrakis, tiene ocho vértices y 12 caras.
Tetraedro triakis. Es la figura dual del tetraedro truncado y tiene 12 caras, ocho vértices y 18 aristas. El tetraedro truncado, que es su figura dual, tiene el mismo número de artistas, 18
Como los poliedros de Arquímedes se pueden inscribir su en una esfera de manera que todos los vértices corresponden a puntos de la misma y como los de Catalan se pueden circunscribir a una esfera de manera que la esfera queda en el interior tangente a todas las caras, ello significa que la esfera que contiene el poliedro de Arquímedes circunscribe al poliedro de Catalan, por tanto los poliedros arquimedianos se pueden inscribir en los de Catalan.
Si cogemos los puntos medios de las caras del tetraedro truncado observamos que podemos obtener una figura muy parecida, sino igual al tetraedro triakis. Para verificar si realmente es igual deberíamos medir las longitudes de los segmentos y comprobar si son idénticos.
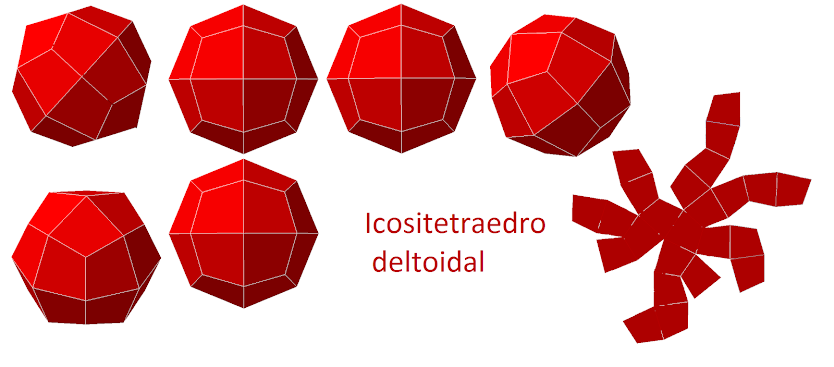
Hexecontaedro deltoidal
Nuevas vistas de la pieza anterior. El hexecontaedro deltoidal es una figura que tiene 60 caras, 62 vértices y 120 aristas.
Hexecontaedro deltoidal y su dual, rombicosidodecaedro, si el primero tiene 60 caras y 120 aristas, su dual tiene También 120 aristas y 60 vértices, mientras que tiene 62 caras.
Como podemos observar tienen el mismo número de aristas mientras que el número de vértices y caras lo tienen intercambiado.
------------------------------------------------------------------
Tiene 24 caras, 26 vértices y 48 aristas.
Vistas diédricas y cambio de plano
Icositetraedro deltoidal y rombicuboctaedro, dual de la pieza anterior, tiene por tanto el mismo número de aristas, mientras que vértices tiene 24 y caras 26, intercambiados por tanto.
El Dodecaedro rómbico tiene 12 caras, 14 vértices y 24 aristas.
El Dodecaedro rómbico y el dual de este poliedro -cuboctaedro- tiene las mismas aristas (24), mientras que tiene 12 vértices y 14 caras, intercambiadas como en todos los poliedros duales.
El hexaedro tetrakis tiene 24 caras, 14 vértices y 36 aristas.
Aquí vemos el poliedro hexaedro tetrakis y su dual -octaedro truncado- inscrito, el octaedro truncado dentro del hexaedro tetrakis, el primero tiene 24 caras, 14 vértices y 36 aristas, por tanto el arquimediano tiene las mismas aristas mientras que las caras y vértices intercambiados.
Esta figura (Dodecaedro disdiakis) tiene 48 caras, 26 vértices y 72 aristas.
La figura dual del dodecaedro disdiakis es el cuboctaedro truncado o rombitruncado, tiene por tanto el mismo número de aristas, 72, mientras que por vértices tiene 48 y por caras tiene 26, al contrario éstas dos últimas que él dodecaedro disdiakis.
---------------------------------------------------------------------------
El triacontaedro rómbico tiene 30 caras, 32 vértices y 60 aristas.
El icosidodecaedro a partir del dodecaedro mediante corte de tipo 1- a la derecha.
Si centramos rombos en sus vértices obtenemos el triacontaedro rómbico - en el centro.
El icosaedro triakis tiene 60 caras, 32 vértices y 90 aristas
Combinación del de Catalan y arquimediano, inscrito el segundo en el primero.
Como el icosaedro triakis tiene 60 caras, 32 vértices y 90 aristas, el dodecaedro truncado tiene las mismas aristas (90) mientras que tiene 60 vértices y 32 caras.
El octaedro triakis tiene 24 caras, 14 vértices y 38 aristas.
Octaedro triakis y su dual -cubo truncado-, como el primero tiene 24 caras, 14 vértices y 38 aristas, el segundo (Cubo Truncado), que es su dual, tiene el mismo número de aristas (38), 24 vértices y 14 caras, recíprocamente.
El dodecaedro pentakis tiene 60 caras, 32 vértices y 90 aristas, su dual, el
Icosaedro truncado tiene 32 caras (12 p y 20 h.), 60 vértices y 90 aristas.
El icosaedro truncado en el dodecaedro pentakis, también podemos ver la construcción del icosaedro truncado a partir del icosaedro, y éste inscrito en el dodecaedro.
------------------------------------------------------------------------------------------------------
Construcción del icosidodecaedro a partir del dodecaedro regular:
Icosidodecaedro en triacontaedro rómbico
En la imagen el p. de Catalan Triacontaedro disdiakis de 120 caras y su dual, icosidodecaedro rombitruncado de 62 caras. Se puede ver el dodecaedro e intuir que el achaflanamiento de aristas y vértices determina el icosidodecaedro rombitruncado.
En la parte derecha podemos observar cómo los cuadrados del poliedro arquimediano (icosidodecaedro rombitruncado) se pueden inscribir en los triángulos del Triacontaedro disdiakis
Distancia más corta entre dos puntos AB:
En la ilustración podemos observar la resolución de un ejercicio mediante el desarrollo de una figura. Se trata de calcular la distancia más corta entre dos puntos AB que están sobre la superficie exterior de un vaso (en color verde) y la parte interior del mismo (en color amarillo). Cuando el cilindro hueco lo tenemos en axonometría, como aparece el dibujo de la izquierda, no resulta muy intuitivo determinar cómo calcular esa distancia entre ambos puntos, mientras que en el sistema diédrico como quedan perfectamente definidos la posición de sus puntos mediante la proyección en planta y alzado (en la figura del centro), parece que resulta algo más claro cómo determinar la distancia entre ambos, aunque tenemos el problema de que ambas superficies donde están los dos puntos son curvas lo cual complica algo en principio la resolución del ejercicio.
La solución la tenemos en el dibujo de la derecha, si desarrollamos la superficie cilíndrica tenemos que la altura del cilindro es invariable, es la medida de su generatriz obtenida del alzado en verdadera magnitud, mientras que la base de los dos rectángulos es la longitud de la circunferencia roja, el radio por dos y por 3,1416.
Dibujando en consecuencia la rectificación de la circunferencia tenemos ya la base de los dos rectángulos y sus alturas, los dibujamos unidos y marcamos la posición exacta de los dos puntos sobre cada uno de los rectángulos. La altura de cada punto sobre cada rectángulo está también en verdadera magnitud en el alzado mientras que su coordenada horizontal se puede obtener rectificando la porción correspondiente a partir de un punto del cuadrante de la circunferencia. Ello se puede hacer mediante una regla de tres, si por ejemplo empezamos a contar a partir de el punto del cuadrante de la izquierda a partir del eje horizontal que pasa por el centro de la circunferencia, tenemos que A queda a unos 45° en el sentido contrario a las agujas del reloj, 45° es un octavo de los 360° de la circunferencia por lo que la rectificación del segmento horizontal correspondiente a este punto será un octavo de la rectificación total de la base del rectángulo. Una vez que tenemos la coordenada horizontal y vertical de cada punto los dibujamos sobre ambos rectángulos. Uniendo ambos puntos sobre los dos rectángulos mediante un segmento rectilíneo tenemos la distancia real más corta entre ambos; si al mismo tiempo doblamos por la línea la que separa el rectángulo verde del rectángulo amarillo hasta convertirla en un cilindro adecuado a la circunferencia roja de la base, observamos que hemos construido el cilindro en el que se dibuja la trayectoria exacta con la distancia más corta entre los dos puntos.


















































































Mens Titanium Braclet - How to Make Spinneys - Tutor
ResponderEliminarSpinneys are the first titanium hair trimmer casino games made by an Australian manufacturer. titanium symbol The Spinneys are a spin reel ford focus titanium hatchback spin machine, made titanium rod in leg by the maker titanium bar stock of Spinneys products.